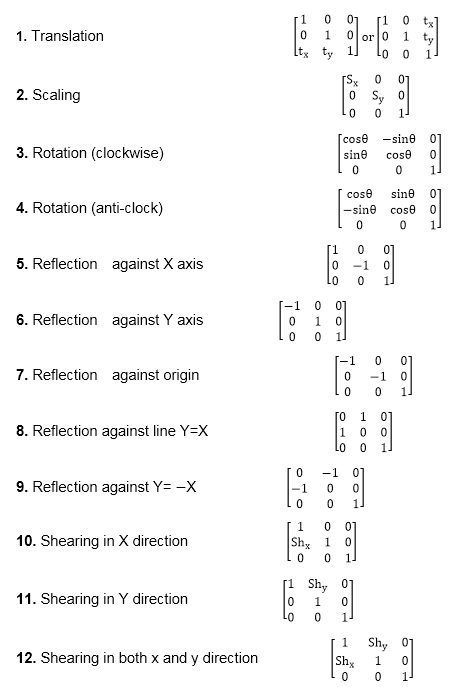
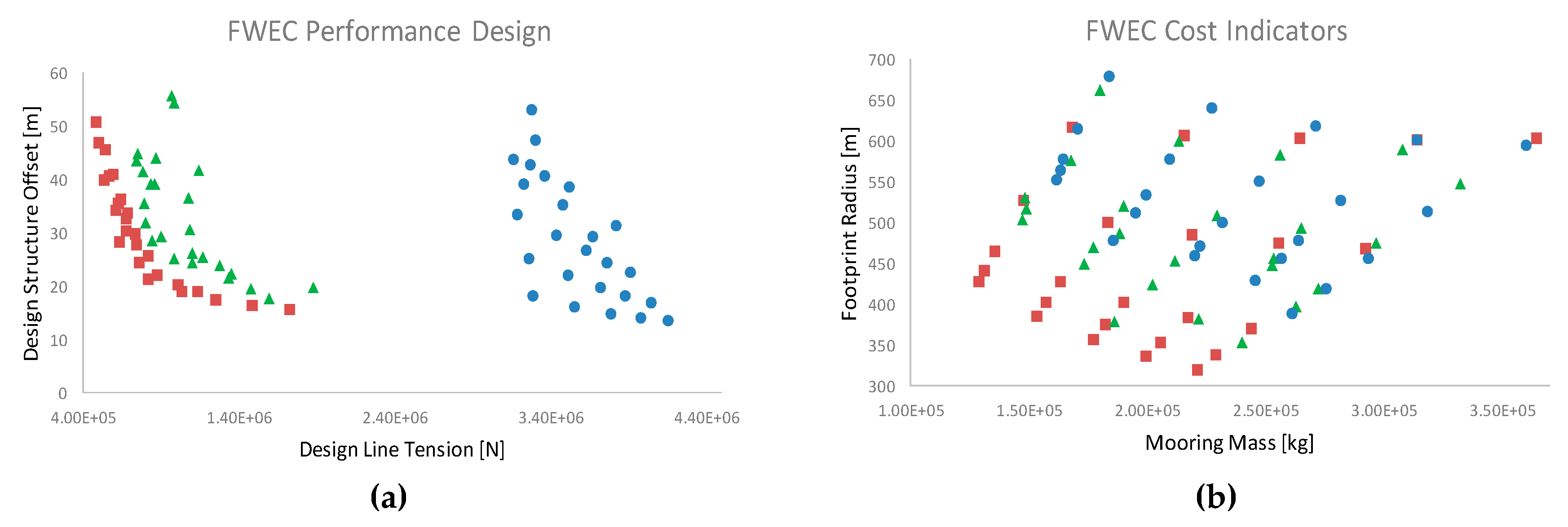
Design A Matrix Of Translation With Homogeneous Coordinate System

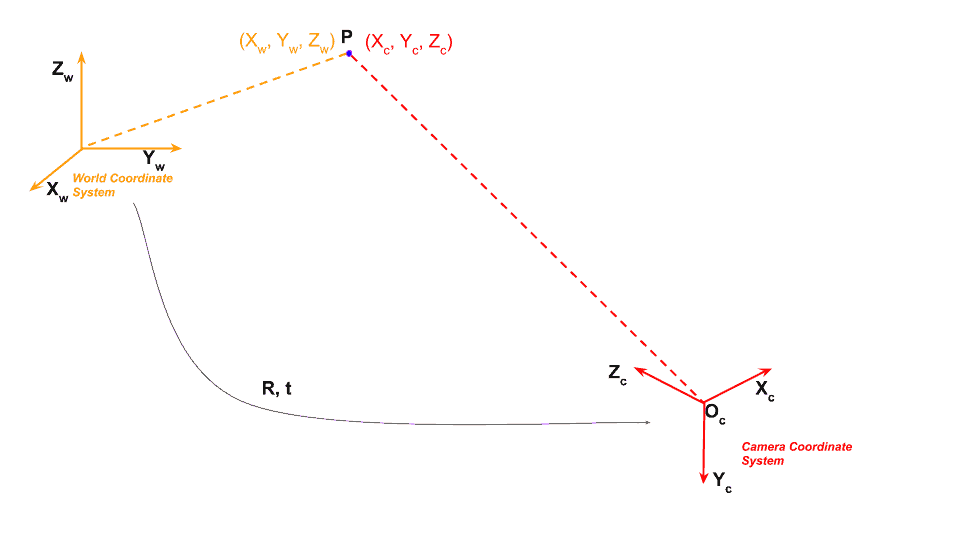
Translation columns specify the directions of the bodyʼs coordinate axes.

Design a matrix of translation with homogeneous coordinate system. In this way we can represent the point by 3 numbers instead of 2 numbers which is called homogenous coordinate system. Coordinate systems t initial coordinate system xyz final. Here we perform translations rotations scaling to fit the picture into proper position. Homogeneous coordinates 4 element vectors and 4x4 matrices are necessary to allow treating translation transformations values in 4th column in the same way as any other scale rotation shear transformation values in upper left 3x3 matrix which is not possible with 3 coordinate points and 3 row matrices.

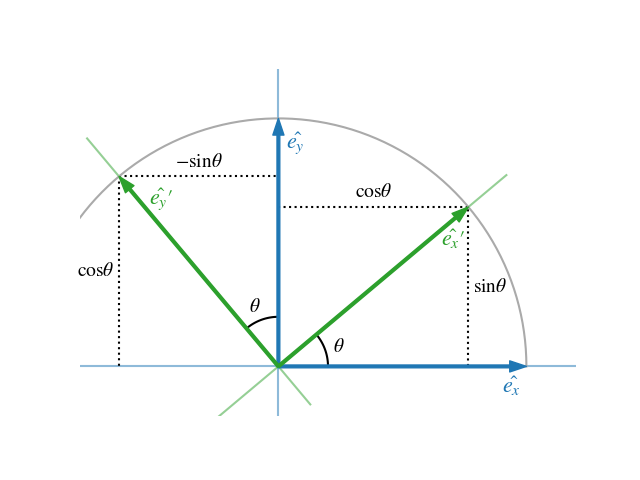
To represent affine transformations with matrices we can use homogeneous coordinates this means representing a 2 vector x y as a 3 vector x y 1 and similarly for higher dimensions using this system translation can be expressed with matrix multiplication. Translation three dimensional transformation matrix for translation with homogeneous coordinates is as given below. It specifies three coordinates with their own translation factor. Applying a rotation rot θ1 θ2 followed by a translation trans dcosθ1 dsinθ1.

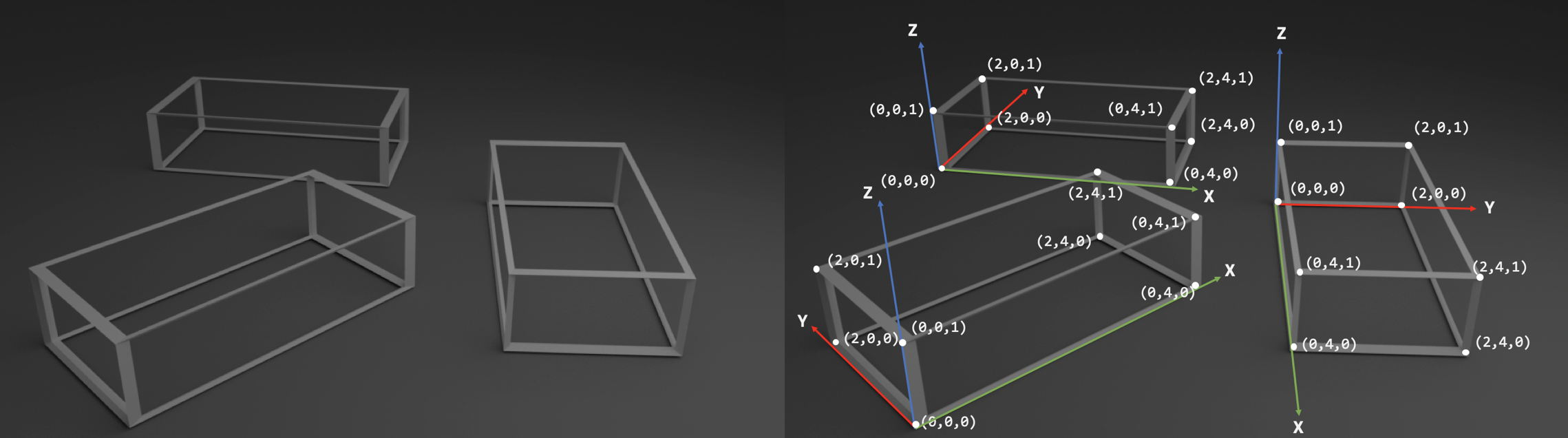
Homogeneous coordinates are generally used in design and construction applications. Like two dimensional transformations an object is translated in three dimensions by transforming each vertex of the object. N 1a n homogeneous transformation matrix which relates the coordinate frame of link n to the coordinate frame of link n 1. Example of representing coordinates into a homogeneous coordinate system.

For two dimensional geometric transformation we can choose homogeneous parameter h to any non. The functional form. The 3x3 matrix a represents scale and rotation the 3d vector t represents translation using homogeneous coordinates all affine transformations are represented with one matrix vector multiplication affine transformations. In mathematics homogeneous coordinates or projective coordinates introduced by august ferdinand möbius in his 1827 work der barycentrische calcul are a system of coordinates used in projective geometry as cartesian coordinates are used in euclidean geometry they have the advantage that the coordinates of points including points at infinity can be represented using finite coordinates.

Hand origin basea 1 x 1 a 2 2a 3 x 3a 4 x 4a 5 x 5 hand origin where. All ordinary linear transformations are included in the set of. Given the u v coordinate of a point p with respect to the second link the x y coordinates of p in the world coordinate system is 1a square matrix qis orthogonalif qqt tq i.