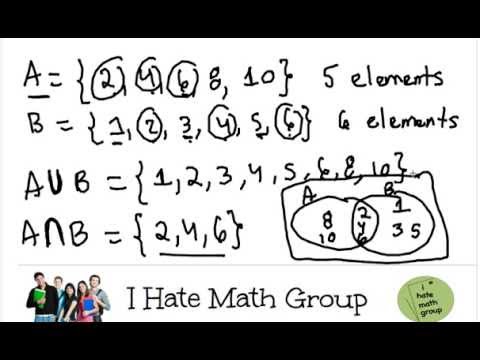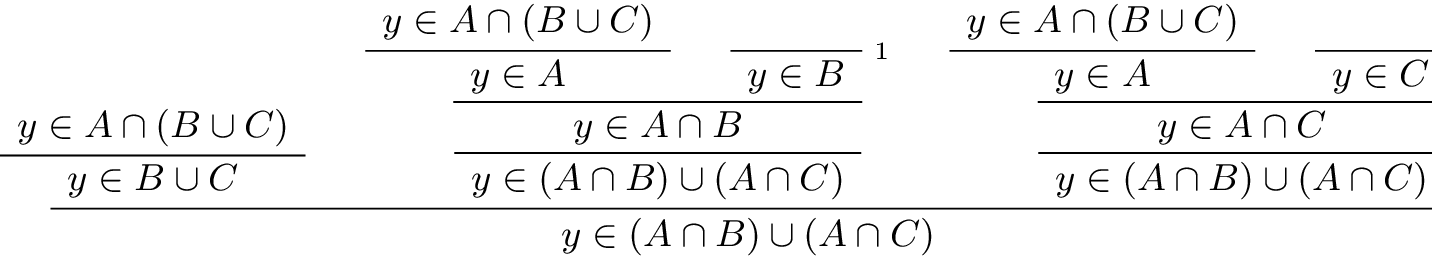Definition Of Intersection In Mathematics

Intersections definition of intersections by the free dictionary.

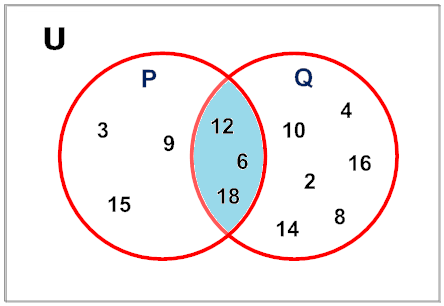
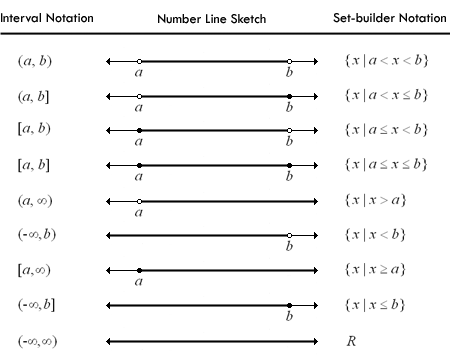
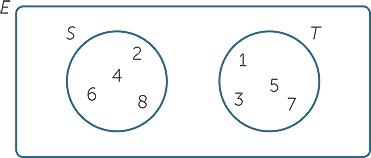
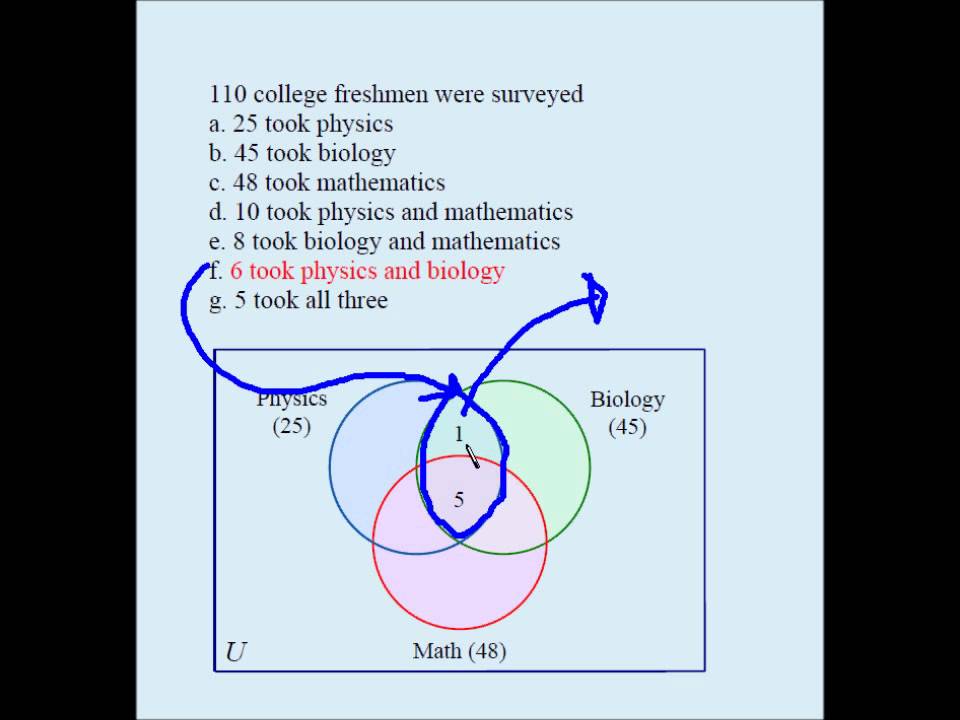
Definition of intersection in mathematics. We write a b c. The intersection of two sets has only the elements common to both sets. The intersection of the sets 3 4 5 6. The intersection of the soccer and tennis sets is just casey and drew only casey and drew are in both sets which can be written.

That is in. Meaning pronunciation translations and examples. The symbol is an upside down u like this. In ter sec tion ĭn tər sĕk shən ĭn tər sĕk n.

A set that contains elements shared by two or more. Where lines cross over where they have a common point. The act process or result of intersecting. A place where things intersect especially a place where two or more roads cross.

Definition of the intersection of two lines. Home contact about subject index. How to use intersection in a sentence. Given three sets a b and c the intersection is the set that contains elements or objects that belong to a b and to c at the same time.

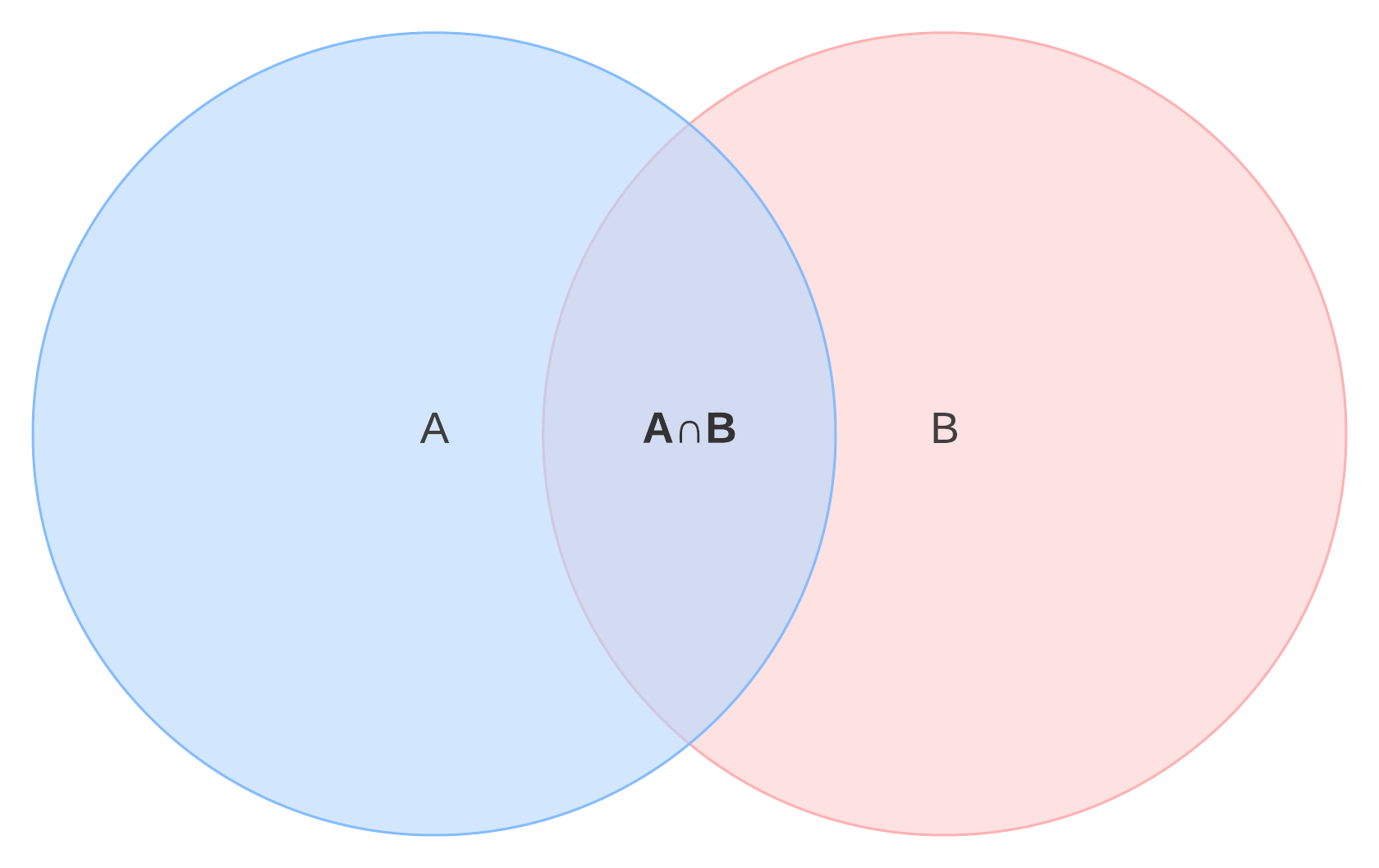
The red and blue lines have an intersection. Intersection definition a place where two or more roads meet especially when at least one is a major highway. Intersection is written using the sign between the terms. If an element is in just one set it is not part of the intersection.

A place where things intersect especially a place where two or more roads cross. An intersection is a place where roads or other lines meet or cross. Intersections synonyms intersections pronunciation intersections translation english dictionary definition of intersections. Intersection definition is a place or area where two or more things such as streets intersect.

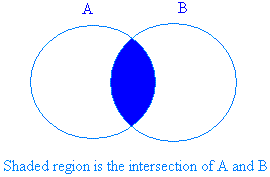
In fact since the empty set is included in any set the intersection of the empty set with any set is the empty set. Definition of the union of three sets. The point or locus of points where one line surface or solid crosses another. In mathematics the intersection of two sets a and b denoted by a b is the set containing all elements of a that also belong to b or equivalently all elements of b that also belong to a.